TIP
嘻嘻,因为可能之后要做一些编译相关的东西,所以准备先熟悉一下 LLVM 和 Rust。在 Rust 里有一个比较好用的 Rust 的 safely binding inkwell,在查找 inkwell 的示例时候找到了一个很多功能未完成的 Rusty Calc (opens new window),因此这次就参考它写一个简简单单的计算器吧~
# 做个什么样的计算器呢?
唔,使用编译原理的话写一个计算器实在是太简单了,毕竟计算器只有简简单单的表达式,而没有那些复杂的语句之类的。虽说简单,但制作一个计算器也是包括了编译的完整流程的,因此拿来练手还是挺合适的~不过重点不是这些,这次我主要的目的是熟悉下 Rust 并了解下 LLVM 的使用方式。
那……要做一个什么样的计算器才合适呢?在开始之前我们首先制定一下计划:
- 它可以运算一些数学表达式,它包含一些常用一元和二元运算符,比如
5 * (6 + 7) / -8 - 它可以访问一些预定义的常量,比如
2 * PI - 它可以使用一些预定义的函数,比如
log(2, 4) - 我们可以为其自定义变量,不过为了简单,我们不需要从文本中专门增加这样一个语句来实现它,而是通过程序 API 在运算前调用实现,比如
define_variable("a", 0.1) - 同样的,我们也可以通过程序里的 API 定义一些函数,比如
define_function("add", |x, y| x + y)
我们可以很轻松写出满足该条件的语法 BNF:
expr ::= <expr> "+" <term>
| <expr> "-" <term>
| <term>
term ::= <term> "*" <term>
| <term> "/" <term>
| <factor-with-unary-op>
factor-with-unary-op ::= "+" <factor-with-unary-op>
| "-" <factor-with-unary-op>
| <factor-with-unary-op> "!"
| <factor>
factor ::= <number>
| <function-call>
| <identifier>
| "(" <expr> ")"
function-call ::= <identifier> "(" <arg-list> ")"
arg-list ::= <empty>
| <expr> ("," <expr>)*
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
这里 expr 就是我们的文法开始符号了,也就是说我们只支持表达式,并通过 term 和 factor 确保乘除优先级高于加减法。为了支持最高优先级的各种一元运算符,因此中间插入了一个 factor-with-unary-op。
# 设计一下 AST 结构
语法已经基本完成,现在我们根据它设计一下 AST 的结构。
# 数字与变量
我们的语法里除了运算符里有两个终结符,分别是 number 和 identifier,我们将它们全放进 Atom 里。
#[derive(Debug, PartialEq, Clone)]
pub enum Atom {
Ident(String),
Number(f64),
}
2
3
4
5
# 运算符
我们的 Atom 之间是通过一些运算符结合在一起的,我们将这里的运算符定义为 Op,而结合后的节点定义为 Arithmetic。
#[derive(Debug, PartialEq, Clone)]
pub enum BinaryOp {
Add,
Sub,
Mul,
Div,
}
#[derive(Debug, PartialEq, Clone)]
pub struct BinaryArithmetic {
pub op: BinaryOp,
pub lhs: Expr,
pub rhs: Expr,
}
2
3
4
5
6
7
8
9
10
11
12
13
14
当然我们既包含一元运算又包含二元运算,但代码基本上是一致的,一元运算就不赘述啦~
# 函数调用
除去这些,我们还有一个 FunctionCall 结点用于表示函数调用,它包含了函数名和函数参数。
#[derive(Debug, PartialEq, Clone)]
pub struct FunctionCall {
pub name: String,
pub args: Vec<Expr>,
}
2
3
4
5
# 表达式结点
当然,最后别忘了我们的顶层表达式结点 Expr
#[derive(Debug, PartialEq, Clone)]
pub enum Expr {
BinaryArithmetic(Box<BinaryArithmetic>),
UnaryArithmetic(Box<UnaryArithmetic>),
Atom(Atom),
FunctionCall(FunctionCall),
}
2
3
4
5
6
7
为了方便,我们为各个结点都实现 Into<Expr> 这一 trait,并为需要的结点实现自己的工厂函数 new
impl BinaryArithmetic {
pub fn new(op: BinaryOp, lhs: Expr, rhs: Expr) -> Self {
BinaryArithmetic { op, lhs, rhs }
}
}
impl Into<Expr> for BinaryArithmetic {
fn into(self) -> Expr {
Expr::BinaryArithmetic(Box::new(self))
}
}
2
3
4
5
6
7
8
9
10
11
# 用 peg 同时完成词法、语法分析
下面我们便开始编写我们的计算器吧~让我想想,编译需要哪些步骤来着?词法分析、语法分析、语义分析、中间代码生成……啊……虽说手写个递归下降分析器也是分分钟的事,但总归还是麻烦,需要写大量重复的代码。而且手写递归下降的话总归还是要面临左递归和左公共因子,所以文法还是需要稍微修改下,可读性可能会因此而降低许多……
嘛,为了解决这些问题,我去找了些 Rust 里的相关 crate,最终决定使用 peg 来做词法、语法分析。
至于为什么用 peg 嘛,主要是它可以直接利用宏直接嵌入在代码里,通过宏自动展开成 rust 代码,而不需要额外编译,另外直接嵌入代码带来最大的优势就是可以实时代码高亮和类型提示。再就是由于 peg 以 PEG 方式解析,因此可以在不改变文法的情况下写左递归和含有左公共表达式的文法。
让我们对照着之前写的 BNF,写一个 peg 的 parser ~
peg::parser! {
pub grammar calc_parser() for str {
use super::Expr;
#[cache_left_rec]
pub rule expr() -> Expr
= a:expr() _ "+" _ b:term() { BinaryArithmetic::new(BinaryOp::Add, a, b).into() }
/ a:expr() _ "-" _ b:term() { BinaryArithmetic::new(BinaryOp::Sub, a, b).into() }
/ term()
#[cache_left_rec]
pub rule term() -> Expr
= a:term() _ "*" _ b:factor_with_unary_op() { BinaryArithmetic::new(BinaryOp::Mul, a, b).into() }
/ a:term() _ "/" _ b:factor_with_unary_op() { BinaryArithmetic::new(BinaryOp::Div, a, b).into() }
/ factor_with_unary_op()
#[cache_left_rec]
pub rule factor_with_unary_op() -> Expr
= "+" _ a:factor_with_unary_op() { UnaryArithmetic::new(UnaryOp::Pos, a).into() }
/ "-" _ a:factor_with_unary_op() { UnaryArithmetic::new(UnaryOp::Neg, a).into() }
/ a:factor_with_unary_op() "!" { UnaryArithmetic::new(UnaryOp::Fac, a).into() }
/ factor()
#[cache]
pub rule factor() -> Expr
= number()
/ function_call()
/ identifier()
/ "(" _ e:expr() _ ")" { e }
pub rule function_call() -> Expr
= id:identifier() _ v:bracketed(<commasep(<expr()>)>) {
FunctionCall::new (
if let Expr::Atom(Atom::Ident(x)) = id { x } else { "".to_owned() },
v
).into()
}
pub rule number() -> Expr
= n:$("-"? ("0" / ['1'..='9']['0'..='9']*) ("." ['0'..='9']+)?) { Atom::Number(n.parse::<f64>().unwrap()).into() }
pub rule identifier() -> Expr
= id:$(['a'..='z' | 'A'..='Z' | '_'] ['a'..='z' | 'A'..='Z' | '0'..='9' | '_']*) { Atom::Ident(id.to_owned()).into() }
rule commasep<T>(x: rule<T>) -> Vec<T> = v:(x() ** ( _ "," _ ) ) ","? { v }
rule bracketed<T>(x: rule<T>) -> T = "(" _ v:x() _ ")" { v }
rule _ = " "*
rule __ = (" " / "\n" / "\r")*
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
emm,和原来的 BNF 基本没有区别嘛,也就多了些生成 AST 的代码。
这样,我们通过 calc_parser::expr 就可以将字符串解析为一棵 AST 了喔~
assert_eq!(
calc_parser::expr("1 + 9 / 10"),
Ok(BinaryArithmetic::new(
BinaryOp::Add,
Atom::Number(1 as f64).into(),
BinaryArithmetic::new(
BinaryOp::Div,
Atom::Number(9 as f64).into(),
Atom::Number(10 as f64).into(),
)
.into()
)
.into())
);
2
3
4
5
6
7
8
9
10
11
12
13
14
# 为 AST 实现 visitor
唔,既然已经得到一棵 AST 了,理所当然我们首先会想如何去遍历它,啊……当然遍历方法是递归啦,其实问题是我们如何去组织这个遍历的代码~
比如我们稍后对各个结点进行 print、check、compile 等等操作,啊这显而易见嘛,既然大家都需要实现这三个函数,那么我们让他们都实现同一个 trait 就好了,这个 trait 要求所有结点都实现这三个函数就 OK 了。
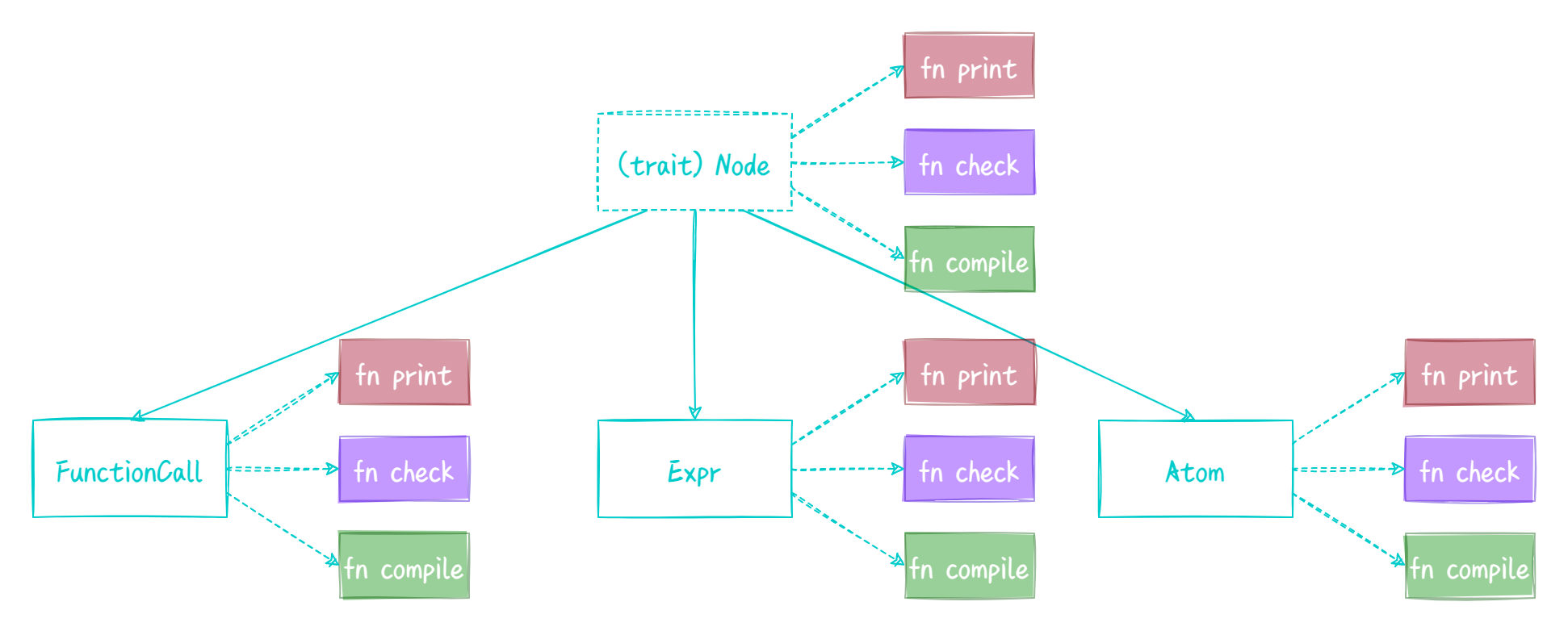
emmm,我们最后实现的代码可能会像上图这样。唔,这样做倒确实可以完成我们的需求啦,但是这样做造成了相同逻辑代码分散在不同的结构体中,所以无论是实现新的逻辑还是修改现有逻辑,我们都得同时修改多个文件……
所以说这种代码组织方式在这里并不是很合适啦,那我们稍微改一下,把每个逻辑放在一起,我们将每个逻辑的集合体称为 Visitor,它将会实现 visit 各种 Node 的方法。

就像上图这样,我们的代码是不是看起来会好很多呢?
那么对于我们的代码,如何实现这样一个 Visitor 也是显而易见了~
pub trait Visitor<T> {
fn visit_expr(&mut self, e: &Expr) -> T;
fn visit_unary(&mut self, u: &UnaryArithmetic) -> T;
fn visit_binary(&mut self, b: &BinaryArithmetic) -> T;
fn visit_function(&mut self, f: &FunctionCall) -> T;
fn visit_atom(&mut self, a: &Atom) -> T;
}
2
3
4
5
6
7
我们实现一个简单的能够帮我们打印树状结构 PrettyPrinter 吧~
pub struct PrettyPrinter {
indent_level: u32,
indent: u32,
}
impl PrettyPrinter {
pub fn new(indent: u32) -> Self {
PrettyPrinter {
indent_level: 0,
indent,
}
}
fn get_indent(&self) -> usize {
(self.indent_level * self.indent) as usize
}
}
impl Visitor<()> for PrettyPrinter {
fn visit_expr(&mut self, e: &Expr) {
let indent = " ".repeat(self.get_indent());
println!("{indent}Expr");
self.indent_level += 1;
match e {
Expr::UnaryArithmetic(ref u) => self.visit_unary(u),
Expr::BinaryArithmetic(ref b) => self.visit_binary(b),
Expr::FunctionCall(ref f) => self.visit_function(f),
Expr::Atom(ref a) => self.visit_atom(a),
}
self.indent_level -= 1;
}
fn visit_unary(&mut self, u: &UnaryArithmetic) {
let indent = " ".repeat(self.get_indent());
match u.op {
UnaryOp::Pos => println!("{indent}Pos"),
UnaryOp::Neg => println!("{indent}Neg"),
UnaryOp::Fac => println!("{indent}Fac"),
}
println!("{indent}Unary");
self.indent_level += 1;
self.visit_expr(&u.value);
self.indent_level -= 1;
}
fn visit_binary(&mut self, b: &BinaryArithmetic) {
let indent = " ".repeat(self.get_indent());
match b.op {
BinaryOp::Add => println!("{indent}Add"),
BinaryOp::Sub => println!("{indent}Sub"),
BinaryOp::Mul => println!("{indent}Mul"),
BinaryOp::Div => println!("{indent}Div"),
}
self.indent_level += 1;
self.visit_expr(&b.lhs);
self.visit_expr(&b.rhs);
self.indent_level -= 1;
}
fn visit_function(&mut self, f: &FunctionCall) {
let indent = " ".repeat(self.get_indent());
let func_name = &f.name;
println!("{indent}Function {func_name}");
self.indent_level += 1;
for arg in &f.args {
self.visit_expr(arg);
}
self.indent_level -= 1;
}
fn visit_atom(&mut self, a: &Atom) {
let indent = " ".repeat(self.get_indent());
match a {
Atom::Ident(ref id) => println!("{indent}Identifier {id}"),
Atom::Number(ref n) => println!("{indent}Number {n}"),
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
嗯,就是这么简单啦,这样我们就可以通过 PrettyPrinter::new(2).visit_expr(ast) 来打印一棵 AST 了~
当然,我们接下来的 Visitor 和这处理方式很相似,其实我们现在距离结束已经非常近啦~
# 简简单单解释器
我们有了 AST,也知道如何去遍历它,那么我们就随时可以求得它的结果啦~
也就是说,我们可以直接针对 AST 通过 rust 代码解释执行,就直接得到结果啦~
# 小小符号表
这其实很简单,其本身没什么可说的,但值得注意的是我们可能需要一个符号表用来存放变量相关信息,由于我们的变量都是事先已知的常量,所以符号表里直接存放对应的值就好。同样的,由于我们的变量只能预先定义,所以也不需要考虑变量作用域的问题,都看作全局变量就好。所以我们的符号表实现起来是非常简单的~
use std::collections::HashMap;
#[derive(Debug)]
pub struct SymbolTable<T> {
map: HashMap<String, T>,
}
#[derive(Debug, PartialEq)]
pub enum SymbolError {
ReDefinition,
UnDefinition,
}
impl<T> SymbolTable<T>
where
T: Copy,
{
pub fn new() -> Self {
SymbolTable {
map: HashMap::new(),
}
}
pub fn define(&mut self, name: &String, value: T) -> Result<(), SymbolError> {
if self.map.contains_key(name) {
return Err(SymbolError::ReDefinition);
}
self.map.insert(name.clone(), value);
Ok(())
}
pub fn get(&mut self, name: &String) -> Result<T, SymbolError> {
if !self.map.contains_key(name) {
return Err(SymbolError::UnDefinition);
}
Ok(*self.map.get(name).unwrap())
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 开始解释吧~
现在我们来实现这个简单的解释器吧~
不过这里实现相对于解释器,其实更像是编译时的常量折叠,因为我们所有叶子结点都是常量,所以常量折叠后就是我们需要的计算结果,但把它看作是针对于 AST 的解释器其实也是无伤大雅的~
pub type Func<T> = fn(Vec<T>) -> T;
#[derive(Debug)]
pub struct Calculator {
variables: SymbolTable<f64>,
functions: SymbolTable<Func<f64>>,
operand_stack: Vec<f64>,
}
#[derive(Debug)]
pub enum CalculatorError {
StackEmpty,
StackNotEmpty,
}
impl Calculator {
pub fn new() -> Self {
Calculator {
variables: SymbolTable::new(),
functions: SymbolTable::new(),
operand_stack: Vec::new(),
}
}
pub fn result(&mut self) -> Result<f64, CalculatorError> {
let value = match self.operand_stack.pop() {
Some(value) => Ok(value),
None => Err(CalculatorError::StackEmpty),
};
if !self.operand_stack.is_empty() {
return Err(CalculatorError::StackNotEmpty);
}
value
}
}
impl Visitor<()> for Calculator {
fn visit_expr(&mut self, e: &Expr) {
match e {
Expr::UnaryArithmetic(ref u) => self.visit_unary(u),
Expr::BinaryArithmetic(ref b) => self.visit_binary(b),
Expr::FunctionCall(ref f) => self.visit_function(f),
Expr::Atom(ref a) => self.visit_atom(a),
}
}
fn visit_unary(&mut self, u: &UnaryArithmetic) {
self.visit_expr(&u.value);
match u.op {
UnaryOp::Pos => (),
UnaryOp::Neg => {
let value = self.operand_stack.pop();
self.operand_stack.push(-value.unwrap());
}
UnaryOp::Fac => {
let value = self.operand_stack.pop();
self.operand_stack
.push(factorial(value.unwrap() as u64) as f64);
}
}
}
fn visit_binary(&mut self, b: &BinaryArithmetic) {
self.visit_expr(&b.lhs);
self.visit_expr(&b.rhs);
let rhs = self.operand_stack.pop().unwrap();
let lhs = self.operand_stack.pop().unwrap();
match b.op {
BinaryOp::Add => self.operand_stack.push(lhs + rhs),
BinaryOp::Sub => self.operand_stack.push(lhs - rhs),
BinaryOp::Mul => self.operand_stack.push(lhs * rhs),
BinaryOp::Div => self.operand_stack.push(lhs / rhs),
}
}
fn visit_function(&mut self, f: &FunctionCall) {
let argc = f.args.len();
for arg in &f.args {
self.visit_expr(arg);
}
let func_name = &f.name;
let func = self.functions.get(func_name).unwrap();
let mut argv = Vec::new();
for _ in 0..argc {
argv.push(self.operand_stack.pop().unwrap());
}
argv.reverse();
self.operand_stack.push(func(argv));
}
fn visit_atom(&mut self, a: &Atom) {
match a {
Atom::Ident(ref id) => self.operand_stack.push(self.variables.get(id).unwrap()),
Atom::Number(ref n) => self.operand_stack.push(*n),
}
}
}
fn factorial(num: u64) -> u64 {
match (1..=num).reduce(|accum, item| accum * item) {
Some(x) => x,
None => num,
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
这里我们通过一个操作数栈来存放计算结果,每次计算得到结果就进行压栈,在遇到运算符时从栈顶取得操作数运算后重新压栈。
当然不用操作数栈直接使用返回值也是可以的,但那太简单啦,就不试啦~(我才不会承认当时没想到利用泛型让 Vistor 实现不同类型的返回值呜呜)
唔,最后实现一下我们当初设计的自定义变量和函数 API ~
impl Calculator {
pub fn define_variable(&mut self, name: &String, value: f64) -> Result<(), SymbolError> {
self.variables.define(name, value)
}
pub fn define_function(&mut self, name: &String, value: Func<f64>) -> Result<(), SymbolError> {
self.functions.define(name, value)
}
}
2
3
4
5
6
7
8
9
现在我们就可以通过下面的方式来自定义变量和函数了~
calculator.define_variable(&"a".into(), 222.0).unwrap();
calculator
.define_function(&"mul".into(), |args| args[0] * args[1])
.unwrap();
2
3
4
嗯,这样我们就可以完成很多很多事情啦~比如预先定义 PI 的值,再比如预先定义 log、sin、cos 等数学函数,这样我们就可以计算各种各样的结果啦~
我们把代码组装一下,现在就可以完成一个非常不错的计算器啦~
fn main() -> Result<(), Box<dyn Error>> {
let input = "log(2, 8) - sin(2 * PI)";
match calc_parser::expr(&input) {
Ok(parsed_input) => {
let mut calculator = Calculator::new();
calculator.preset().unwrap();
calculator.define_variable(&"PI".into(), consts::PI).unwrap();
calculator.define_function(&"log".into(), |argv| f64::log(argv[1], argv[0])).unwrap();
calculator.visit_expr(&parsed_input);
let result = calculator.result().unwrap();
println!("Calculator Interpret result: {result}");
}
Err(e) => {
let (err_line, err_col) = (e.location.line, e.location.column);
let error_line = input.split("\n").collect::<Vec<_>>()[err_line - 1];
println!(
"Unexpected char `{}` at line {}, column {}:",
error_line.chars().nth(err_col - 1).unwrap(),
err_line,
err_col
);
println!("{}", error_line);
println!("{}{}", " ".repeat(err_col - 1), "^");
println!("Excepct chars: {:?}", e.expected);
Ok(())
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
上面代码最后应当能够计算得到正确的结果 3.0000000000000004~
啊,完事啦完事啦~我们这就做完一个计算器啦~~~
诶?等会,好像忘了点东西啊,我们的主角 LLVM 呢???
# 用 LLVM 来 JIT 编译一下吧~
当然,如果只是一个计算器的话,解释执行完全足够了,编译完全是没必要的,但目的是练手嘛~所以 LLVM 这时候就要强行登场啦~
不过此前我对 LLVM 是基本不了解的,所以代码基本都是直接参考的 inkwell 里的 example 和 Rusty Calc,剩下的是看文档猜的……
# inkwell 的基本结构
首先我们先把一些基本的属性确定下来,比如 LLVM 里的 context、module、builder 什么的。然后,我们实现一个只能计算数字常量最简 JIT 编译器,这个直接参考 inkwell 的 JIT example 就可以写出来~
pub type CalcMain = unsafe extern "C" fn() -> f64;
pub const CALC_ENTRYPOINT: &str = "calc_main";
#[derive(Debug)]
pub struct CalculatorJIT<'ctx> {
context: &'ctx Context,
module: Module<'ctx>,
builder: Builder<'ctx>,
execution_engine: ExecutionEngine<'ctx>,
}
impl<'ctx> CalculatorJIT<'ctx> {
pub fn new(context: &'ctx Context) -> Self {
let module = context.create_module("calc");
let execution_engine = module
.create_jit_execution_engine(OptimizationLevel::None)
.unwrap();
CalculatorJIT {
context: &context,
module,
builder: context.create_builder(),
execution_engine,
}
}
#[inline]
fn double(&self) -> FloatType<'ctx> {
self.context.f64_type()
}
pub fn compile(&mut self, ast: &Expr) -> Option<JitFunction<CalcMain>> {
let sig = self.double().fn_type(&[], false);
let func = self.module.add_function(CALC_ENTRYPOINT, sig, None);
let basic_block = self.context.append_basic_block(func, "entry");
self.builder.position_at_end(basic_block);
let ret = self.visit_expr(ast);
self.builder.build_return(Some(&ret));
unsafe { self.execution_engine.get_function(CALC_ENTRYPOINT).ok() }
}
}
impl<'ctx> Visitor<FloatValue<'ctx>> for CalculatorJIT<'ctx> {
fn visit_expr(&mut self, e: &Expr) -> FloatValue<'ctx> {
match e {
Expr::UnaryArithmetic(ref u) => self.visit_unary(u),
Expr::BinaryArithmetic(ref b) => self.visit_binary(b),
Expr::FunctionCall(ref f) => self.visit_function(f),
Expr::Atom(ref a) => self.visit_atom(a),
}
}
fn visit_atom(&mut self, a: &Atom) -> FloatValue<'ctx> {
match a {
Atom::Ident(ref id) => unimplemented!(),
Atom::Number(ref n) => self.double().const_float(*n),
}
}
}
fn main() -> Result<(), Box<dyn Error>> {
let input = "1.1";
match calc_parser::expr(&input) {
Ok(parsed_input) => {
let context = Context::create();
let mut calculator_jit = CalculatorJIT::new(&context);
let calc_main = calculator_jit.compile(&parsed_input).unwrap();
let result = unsafe { calc_main.call() };
println!("JIT compile result: ");
}
Err(e) => unimplemented!(),
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
不出意外,上面的代码是可以直接计算得到结果 1.1 的。
那我们 JIT 编译到底有什么用呢?其实这里我们编译得到的 calc_main 以后是可以重复调用的,不必每次都从 AST 解释计算。
# 用 builder 构建运算
下面我们逐渐完善计算相关的代码
impl<'ctx> Visitor<FloatValue<'ctx>> for CalculatorJIT<'ctx> {
fn visit_unary(&mut self, u: &UnaryArithmetic) -> FloatValue<'ctx> {
let value = self.visit_expr(&u.value);
match u.op {
UnaryOp::Pos => value,
UnaryOp::Neg => self.builder.build_float_neg(value, "neg"),
UnaryOp::Fac => unimplemented!(),
}
}
fn visit_binary(&mut self, b: &BinaryArithmetic) -> FloatValue<'ctx> {
let lhs = self.visit_expr(&b.lhs);
let rhs = self.visit_expr(&b.rhs);
match b.op {
BinaryOp::Add => self.builder.build_float_add(lhs, rhs, "add"),
BinaryOp::Sub => self.builder.build_float_sub(lhs, rhs, "sub"),
BinaryOp::Mul => self.builder.build_float_mul(lhs, rhs, "mul"),
BinaryOp::Div => self.builder.build_float_div(lhs, rhs, "div"),
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
一元运算二元运算都很简单,直接通过 builder 里的操作构建相关的代码就好,不过阶乘这样复杂的操作暂时是没办法完成的。
嗯,现在我们应该能做一些复杂的运算了,比如 1 * 2 / -4 等等。
# 定义全局变量
下面我们支持一下变量吧,由于我们的变量都是预先定义好的,因此可看作全局变量,其地址可存在符号表之中,
#[derive(Debug)]
pub struct CalculatorJIT<'ctx> {
// 增加变量符号表属性
variables: SymbolTable<PointerValue<'ctx>>,
}
impl<'ctx> CalculatorJIT<'ctx> {
pub fn define_variable(&mut self, name: &String, value: f64) -> Result<(), SymbolError> {
let var = self
.module
.add_global(self.double(), Some(AddressSpace::Global), name);
// 赋初值
let initial_value = self.double().const_float(value);
var.set_initializer(&initial_value);
// 获取地址
let alloca = var.as_pointer_value();
self.variables.define(name, alloca)?;
Ok(())
}
fn get_variable(&mut self, name: &String) -> Result<FloatValue<'ctx>, SymbolError> {
// 直接从符号表取得地址
let alloca = self.variables.get(name)?;
let var = self
.builder
.build_load(alloca, name.as_str())
.into_float_value();
Ok(var)
}
}
impl<'ctx> Visitor<FloatValue<'ctx>> for CalculatorJIT<'ctx> {
fn visit_atom(&mut self, a: &Atom) -> FloatValue<'ctx> {
match a {
// 增加变量的处理
Atom::Ident(ref id) => self.get_variable(id).unwrap(),
Atom::Number(ref n) => self.double().const_float(*n),
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# 定义函数
函数的定义也很相似,这里同样为了方便定义函数,也使用闭包的形式,不过为了方便闭包里构建各种操作,所以把 builder 也一并传入。
pub type FuncLLVM<'a, T> = fn(Vec<T>, &Builder<'a>) -> T;
impl<'ctx> CalculatorJIT<'ctx> {
pub fn define_function(
&mut self,
name: &String,
argc: usize,
func: FuncLLVM<'ctx, FloatValue<'ctx>>,
) -> Result<(), SymbolError> {
let ret_type = self.double();
let args_types = std::iter::repeat(ret_type)
.take(argc)
.map(|f| f.into())
.collect::<Vec<BasicMetadataTypeEnum>>();
let args_types = args_types.as_slice();
let fn_type = self.double().fn_type(args_types, false);
let fn_val = self.module.add_function(name.as_str(), fn_type, None);
let entry = self.context.append_basic_block(fn_val, "entry");
self.builder.position_at_end(entry);
let mut args = Vec::with_capacity(argc);
for i in 0..argc as u32 {
args.push(fn_val.get_nth_param(i).unwrap().into_float_value())
}
let ret_val = func(args, &self.builder);
self.builder.build_return(Some(&ret_val));
Ok(())
}
pub fn get_function(&mut self, name: &String) -> Result<FunctionValue<'ctx>, SymbolError> {
match self.module.get_function(name) {
Some(func) => Ok(func),
None => Err(SymbolError::UnDefinition),
}
}
}
impl<'ctx> Visitor<FloatValue<'ctx>> for CalculatorJIT<'ctx> {
fn visit_function(&mut self, f: &FunctionCall) -> FloatValue<'ctx> {
let argc = f.args.len();
let func = self.get_function(&f.name).unwrap();
let mut argv = Vec::with_capacity(argc);
for i in 0..argc {
argv.push(self.visit_expr(&f.args[i]))
}
let argsv: Vec<BasicMetadataValueEnum> =
argv.iter().by_ref().map(|&val| val.into()).collect();
let ret_val = self
.builder
.build_call(func, argsv.as_slice(), "tmp")
.try_as_basic_value()
.left()
.unwrap();
ret_val.into_float_value()
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
嘛,虽然看着挺麻烦的,不过参考 example 还是很容易写出来的~
现在我们就可以自己定义常量和函数啦~
calculator_jit.define_variable(&"a".into(), 222.0).unwrap();
calculator_jit
.define_function(&"mul".into(), 2, |args, builder| {
let a = args[0];
let b = args[1];
builder.build_float_mul(a, b, "mul")
})
.unwrap();
2
3
4
5
6
7
8
不过实现 log、sin 这种函数还是不太行啦,只能实现一些非常简单的函数。
总算是完成啦,到此为止我们不仅快速实现了一个解释型的计算器,还实现了一个与其基本功能一致的 JIT 编译型的计算器~
代码就扔到 ShigureLab/rcalc (opens new window) 咯~溜了溜了~