Maxout 的简单理解与实现

TIP

Maxout 是 Goodfellow 在 2013 年提出的一个新的激活函数，相比于其它的激活函数，Maxout 本身是需要参数的，参数可以通过网络的反向传播得到学习，相应地，它比其它激活函数有着更好的性能，理论上可以拟合任意凸函数，进而使得网络取得更好的性能

预备知识
- 基本全连接与卷积网络连接方式
- TensorFlow V2 的基本使用
开发环境
- python 3.6

# 1 什么是 Maxout

Maxout 可以说是一个激活函数，但与其他激活函数所不同的是，它本身是拥有参数的，正因为此，它可以拟合任意的凸函数，那么它是如何实现的呢？

首先我们弄清一个问题，卷积层在通道阶上和全连接层并没有任何区别，只是额外在图像的两个阶增加了卷积核的稀疏连接，但这往往是很小的（ $3 \times 3$ ， $5 \times 5$ 这样），所以说我们只考虑卷积网络的最后一个阶的话，它与全连接并无区别，这里就直接使用全连接网络作为例子，当然，卷积网络也是适用的

我们网络前层进行 $WX + b$ 的线性变换后，是需要增加激活函数进行非线性变换的，但是具体怎么选择激活函数呢？我们可不可以让网络自己学习这个呢？

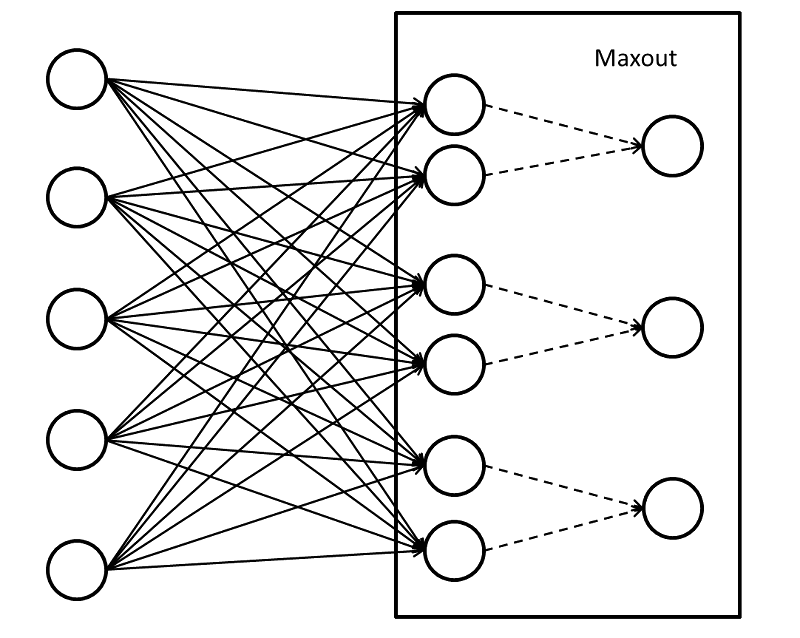
上图便是最基本的 $Maxout$ 连接示意图，前面与普通的全连接并无区别，之后每两个单元“连接”到一个单元上，当然，这里不是真的连接，因为该条线上并不涉及参数，那么如何从两个单元得到一个单元的值呢？其实只需要比较两个单元的值即可，大的值便可以通过~也便是 $Max\ Out$

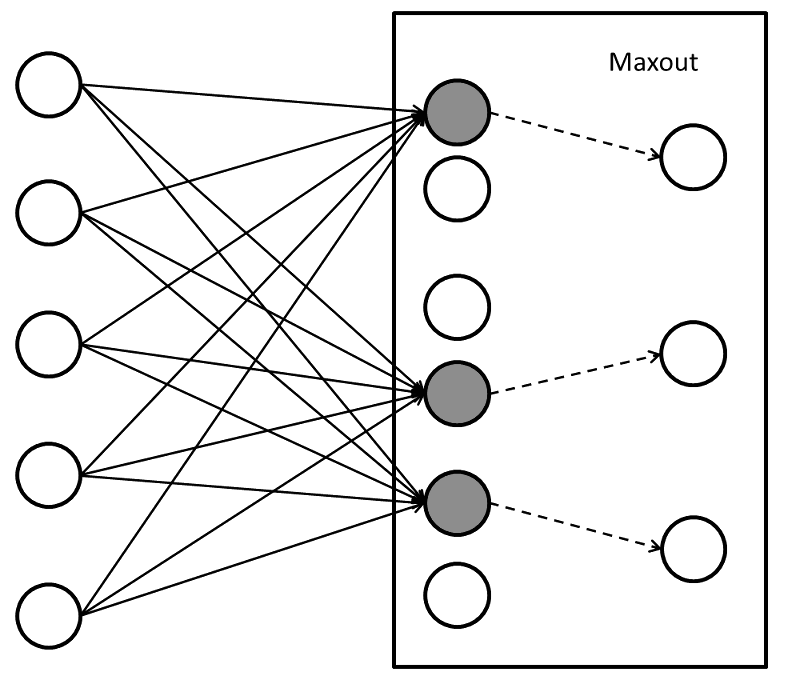
结果便如上图所示，每两个单元中较大的值会被激活

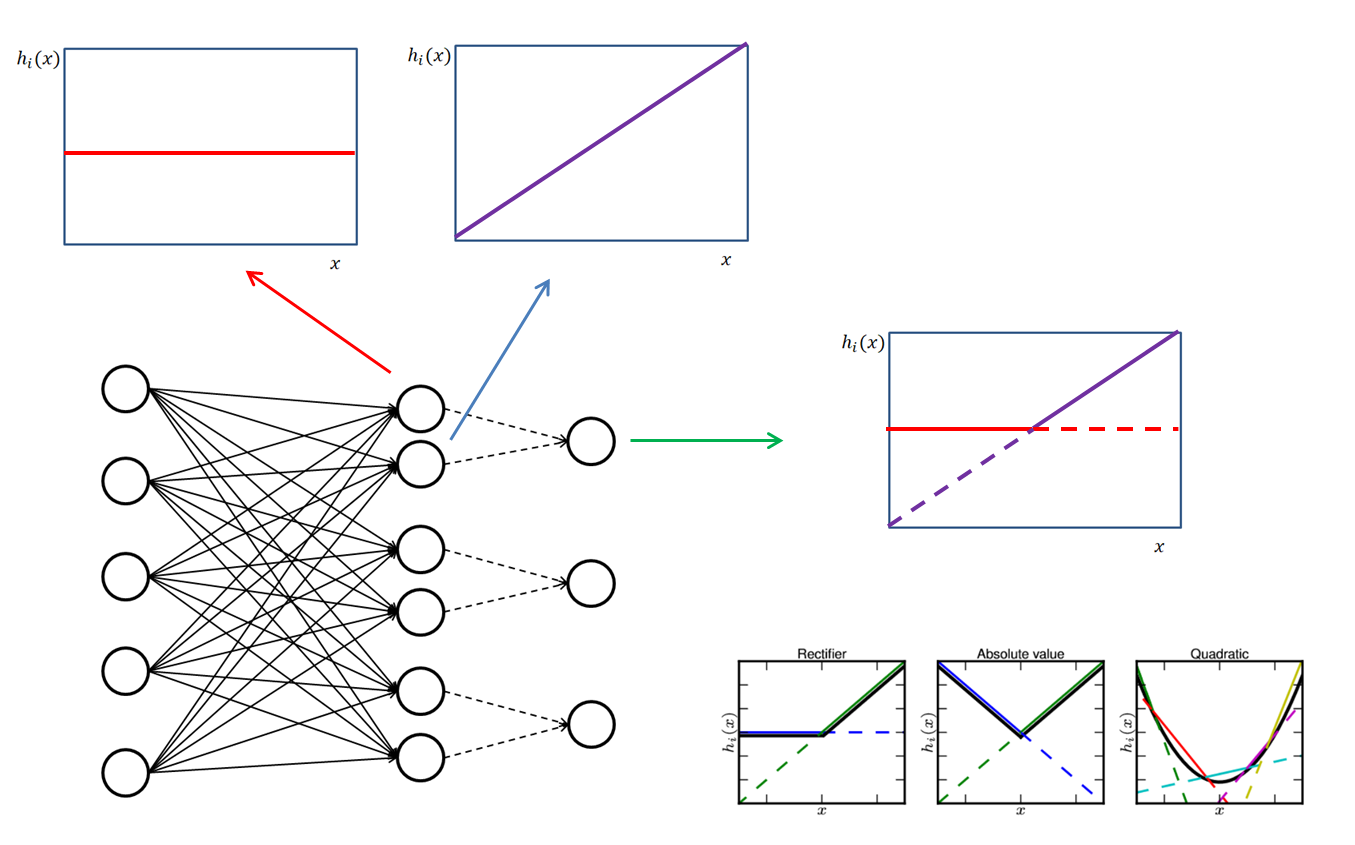
我们知道每个单元都是前层特征的线性组合，那么比如上图中第一个单元学习到了 $y = 0$ ，而第二个单元学习到了 $y = x$ ，那么这两个单元学习到的激活函数便是 $ReLU$ 激活函数

更一般地，我们使每 $k$ （前面的例子 $k = 2$ ）个单元“连接”到一个单元上，那么 $Maxout$ 可以学习到更多段的分段函数作为激活函数，当 $k$ 足够大时，理论上可以拟合任何凸函数

# 2 如何实现 Maxout

一种很直觉的方法就是，我们先将原本的 $m$ 个参数改为 $m \times k$ 个参数，之后每组挑取最大的，但是这样的话，就需要预先用一个矩阵对原先的参数进行线性变换，增加了实现的复杂性

我们反过来想，如果前一层的输出已经是 $m \times k$ 个参数了呢？很简单。我们 $Maxout$ 只需要分组并每个组选一个最大值就好了嘛~这里参考 TensorFlow1.13 版本的 tf.contrib.layers.maxout ，使用 TensorFlow V2 的 tf.keras.layers.Layer API 重写了下

import tensorflow as tf
class Maxout(tf.keras.layers.Layer):
    def __init__(self, units, axis=None):
        super().__init__()
        self.units = units
        self.axis = axis
        if axis is None:
            self.axis = -1
    def build(self, input_shape):
        self.num_channels = input_shape[self.axis]
        assert self.num_channels % self.units == 0
        self.out_shape = input_shape.as_list()
        self.out_shape[self.axis] = self.units
        self.out_shape += [self.num_channels // self.units]
        for i in range(len(self.out_shape)):
            if self.out_shape[i] is None:
                self.out_shape[i] = -1
    def call(self, inputs):
        x = tf.reduce_max(tf.reshape(inputs, self.out_shape), axis=-1)
        return x
# x.shape = (..., d)
x = tf.keras.layers.Conv2d(k * m, kernel_size, strides, padding)(x)
# x.shape = (..., m*k)
x = Maxout(num_units=m)(x)
# x.shape = (..., m)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

这种实现方式可以让我们像加一个激活函数一样把 $Maxout$ 加到网络中，但是值得注意的是，这样的 $Maxout$ 实现会将 $m \times k$ 个单元减少为 $m$ 个

# 1 什么是 Maxout

# 2 如何实现 Maxout

# References