模拟退火算法

TIP

神经网络优化的最大难题就是很容易陷入局部最优，前段时间考虑神经网络优化方法的时候偶然考虑到了这样一个问题：能量为什么总是能达到最低呢？该问题促使我展开了一系列的思（xia）考（xiang），当然，瞎想也没想出个啥，直到今天遇到了模拟退火算法……

# 为什么能量总能达到最低？

这是一个热力学问题，能量也是有着局部最优的，但由于分子的热运动导致一部分分子能够跨越势垒进而达到更低的能量状态，而跨越势垒的分子数满足一定的概率分布（阿伦尼乌兹公式）

（这段纯属胡说八道，可以跳过）咦？原来是这样呀，我想了一段时间后得出了结论：概率分布嘛，那感觉有点 Monte Carlo 的感觉了，分子是比较多的嘛，那么整体的能量总会是最低的，就类似于 Ensemble 那样咯，网络宽一些会更好？

咳咳，好了进入正题，今天才发现根据前面的阿伦尼乌兹公式，有着一种启发式搜索算法，其名为模拟退火算法，嗯，一听名字倍感亲切啊，这不就是我专业学的吗~那么到底什么是模拟退火算法呢？这到底是不是金属热处理中所说的那种退火呢？

# 啥是退火？

就材料加工而言，工业上常说有四把火，分别是退火、正火、淬火、回火，这里举两个极端的例子

一是淬火，这个大家应该也不会陌生，应该都有见过将烧热的金属放入冷水中淬炼的相关场景。很明显，这是使得金属温度骤降，进而内部发生某些变化以达到更高的硬度（具体原因不详细说明），但是这对于金属本身而言，它的能量并不是最低的（稳定相），而是陷入某些局部最低点（亚稳相），这有点像我们使用 BP 等优化算法陷入的局部最优解

另一个就是今天的主角退火啦，虽然淬火后有些性能（比如硬度）是比较好的，但其他性能可能会很差，退火是为了让金属达到能量最低的状态（稳定相），与淬火相反的是，我们只需要缓慢地降低温度，它总能达到能量最低的状态（稳定相）

那么为什么只要温度降低的足够慢它就能达到能量最低的状态呢？这还要从热力学说起

# 相变势垒

我们优化时最大的障碍就是局部最优与全局最优之间的一个或多个“势垒”，热力学中也是这样，但分子（或原子）是有能力跨过这个势垒的，如下图所示

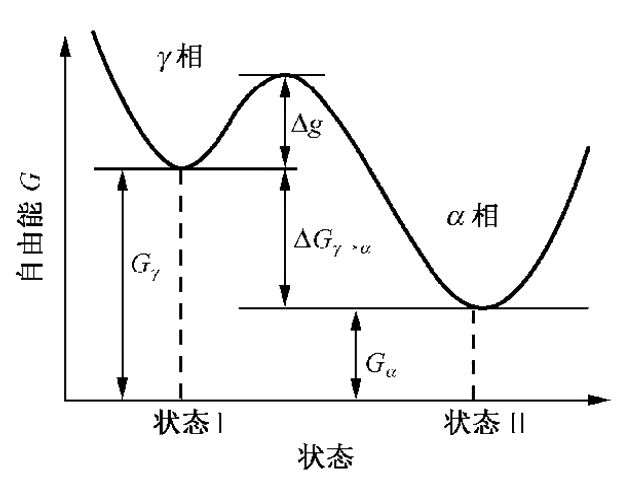
SPT02

当分子处于 $\gamma$ 相时，每个分子并不会乖乖地待在原地不动，而是会根据分子的热运动以一定的概率跨过壁垒到达 $\alpha$ 相，这个现象使用阿伦尼乌兹公式描述

K = K_0 exp[-\frac{Q}{kT}]

其中 $K_0$ 是原 $\gamma$ 相的总分子数， $K$ 是其中转变为 $\alpha$ 相的分子数，由于是分子热运动， $T$ 自然就是温度，另外，由于势垒越高越难以跨越，所以这里的 $Q$ 就是势垒能量值，也就是上图中的 $\Delta g$ ， $k$ 是一个常数，当然，我们“爬山”的概率就是后面的 $exp[-\frac{Q}{kT}]$ 这一部分

emmmm，那么退火时候为什么总能收敛到全局最优呢？这样看的话，最主要的原因就是其拥有以一定概率跨过壁垒的能力

# 一般的优化算法

在说退火在优化算法上的应用之前，先说一下其他的优化算法

# Monte Carlo

第一种是一种最最最简单的算法，就是在可行解空间内不断地随机 sample 一些点出来，然后找到一个最小值就好了嘛，emmm，它的优点是没什么陷入全局最优的问题，但缺陷也很明显，当可行解空间比较大时，能 sample 到什么样的点就只能看脸了

# 爬山算法

然后我们使用稍微高级一点的，爬山算法（为了保持一致，我这里是向全局最小优化的，或者我们可以叫作“爬坑算法”），这个有点类似于 BP，但是并不需要求梯度，它只不过是将 BP 优化中的“向梯度最小的方向移动一步”改成了“随机看看周围某一个位置的情况，如果比当前位置低则移到该位置”，实现起来非常简单，就像这样


import numpy as np
import matplotlib.pyplot as plt
X_BOUND = [-2, 5]
def F(x):
    return x*(x-1)*(x-2)*(x-4)
num_epochs = 10000
x_set = []
initial_value = np.random.uniform(*X_BOUND, size=1)
x = initial_value.copy()
y = F(x)
for i in range(num_epochs):
    # 随机移动的方向
    dx = learning_rate * (X_BOUND[1] - X_BOUND[0]) * (2*np.random.random()-1)
    y_new = F(x+dx)
    # 如果更低则移动
    if y_new < y:
        y = y_new
        x += dx
        x_set.append(x.copy())
best = x + dx
x = np.linspace(*X_BOUND, 200)
plt.plot(x, F(x))
plt.scatter(np.array(x_set), F(np.array(x_set)), c='r')
plt.scatter(initial_value, F(initial_value), c='white')
plt.scatter(best,F(best), c='black')
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

SA01

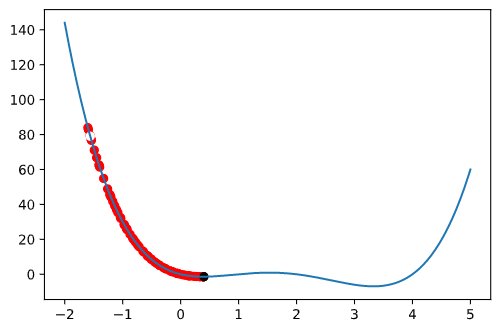
实现是很简单，但是这样很容易陷入局部最优，然后就再也跳不粗来了~

# 模拟退火算法

如果我们给爬山算法一种以一定概率走向能量更高的位置的能力，是不是就很像分子热运动了？至于概率嘛，就是前面的阿伦尼乌兹公式里的 $exp[-\frac{Q}{kT}]$ 啦，不过由于 $k$ 只是一个常数，我们可以合并到 $T$ 中，由于我们要模拟金属的缓慢冷却，温度是需要缓慢衰减的，至于衰减方法嘛是有很多的，比如每次变成上次的 0.99 倍之类，这里使用 $T(k) = \frac{T(0)}{\ln (1 + k)}$ 这种衰减方案，其中 $k$ 表示迭代次数

代码很简单，简单改改就好了

--- sa01.py             2021-01-04 17:04:26.000000000 +0800
+++ sa02.py             2021-01-04 17:06:18.000000000 +0800
@@ -6,6 +6,8 @@
 def F(x):
     return x*(x-1)*(x-2)*(x-4)

+t0 = 5.0
+t = t0
 num_epochs = 10000
 learning_rate = 0.01
 x_set = []
@@ -23,6 +25,17 @@
         y = y_new
         x += dx
         x_set.append(x.copy())
+    # 如果更高则以一定概率移动
+    else:
+        prob = 1.
+        if t != 0:
+            prob = np.exp((y - y_new) / t)
+        if prob >= np.random.random():
+            y = y_new
+            x += dx
+            x_set.append(x.copy())
+    # 冷却
+    t = t0 / np.log(1 + i)

 best = x + dx

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

SA02

从图中确实可以看出，模拟退火算法有着更好的跳出局部最优的能力（图中白点为起始点，黑点为最终点）

# 更一般的猜想

为什么分子热运动会以那样的概率跨过势垒呢？是不是因为每个分子都会以一定的概率跳到某个能量的位置呢？如果这么想的话，便有

\begin{aligned} P(E > E_0 + Q) &= e^{-\frac{Q}{kT}} \\ P(E \leq E_0 + Q) &= 1 - e^{-\frac{Q}{kT}} \end{aligned}

嘛，这不是指数分布嘛，那么我们完全可以算出达到某一能量的概率

P(E = E_0 + Q) = -\frac{1}{kT} e^{-\frac{Q}{kT}}

那么，我们以指数分布得到一个能量值 $Q$ ，将 $E_0 + Q$ 作为当前可能达到的能量值，直接与 sample 到的下一个位置真实能量值作比较，如果比它大则移动，这样实现的话会更加简单些，这里展示下与爬山算法不同的地方

--- sa01.py             2021-01-04 17:04:26.000000000 +0800
+++ sa03.py             2021-01-04 17:07:19.000000000 +0800
@@ -6,6 +6,8 @@
 def F(x):
     return x*(x-1)*(x-2)*(x-4)

+t0 = 5.0
+t = t0
 num_epochs = 10000
 learning_rate = 0.01
 x_set = []
@@ -18,11 +20,15 @@
     # 随机移动的方向
     dx = learning_rate * (X_BOUND[1] - X_BOUND[0]) * (2*np.random.random()-1)
     y_new = F(x+dx)
+    # 分子热运动所带来的“能量”，sample 自指数分布
+    delta_y = np.random.exponential(t, size=1)
     # 如果更低则移动
-    if y_new < y:
+    if y_new < y + delta_y:
         y = y_new
         x += dx
         x_set.append(x.copy())
+    # 冷却
+    t = t0 / np.log(1 + i)

 best = x + dx

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

SA03

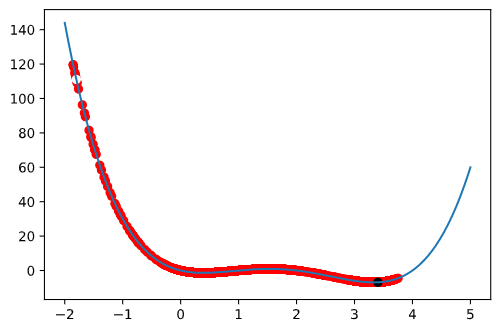
是不是非常简单，而且效果确实和模拟退火算法一样呢，这样的话，也许这种实现能够很容易地和其它优化算法相结合（替换掉爬山算法），以达到更好的效果